Одна из самых известных и важных теорем в математике помогает понять взаимосвязь между сторонами прямоугольного треугольника. Рассказываем, кто такой Пифагор, как работает его теорема, а также рассматриваем несколько практических примеров.
Кто такой Пифагор
Это древнегреческий ученый и философ, создатель школы пифагорейцев и автор множества научных открытий. О его жизни сохранилось множество легенд и совсем мало точных фактов.
Пифагор родился около 570 года до н. э. на острове Самос. Много лет он провел за пределами родины, путешествуя и познавая разные науки. Из-за политических гонений Пифагор вынужден был уехать в Италию, где основал собственную религиозно-философскую школу.
Идеи Пифагора оказали огромное влияние на развитие науки в целом и математики в частности. Например, он создал учения о подобии геометрических фигур, построении правильных многоугольников и прямолинейных фигур, четных и нечетных числах и многие другие теории и доказательства.
Философу также присваивают авторство известной теоремы о соотношении сторон в прямоугольном треугольнике. На самом деле она была известна задолго до Пифагора. Например, древние египтяне знали, что треугольник со сторонами 3, 4 и 5 является прямоугольным, и использовали его параметры при построении зданий и межевании земель (1).
Считается, что древнегреческий математик или кто-то из его учеников сумел доказать теорему и передал это знание людям. Существует легенда, что Пифагор очень обрадовался открытию и в благодарность принес богам в жертву сотню быков (2).
О чем гласит теорема Пифагора: суть простыми словами
Каждый прямоугольный треугольник состоит из трех сторон, которые носят отдельные названия. Сторона, лежащая напротив прямого угла, называется гипотенузой. Линии, которые пересекаются под углом 90°, — катетами.
Катеты всегда меньше гипотенузы — это видно невооруженным глазом. Пифагор сумел установить правильное соотношение этих сторон и доказал, что если возвести длину каждого катета в квадрат, а затем сложить — получится значение гипотенузы в квадрате.
Формула теоремы Пифагора
Если обозначить катеты a и b, а гипотенузу — c, получится следующая формула:
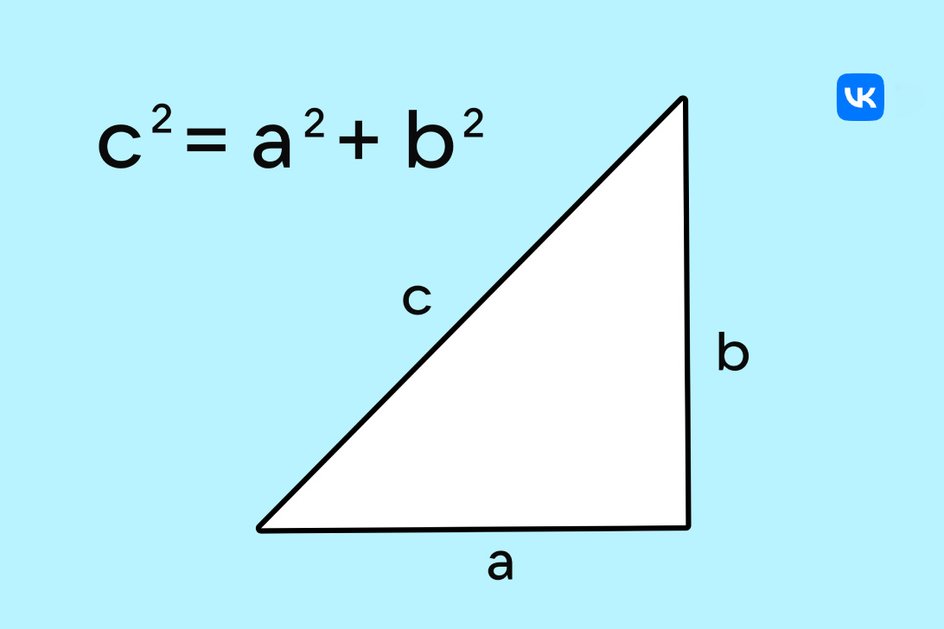
Из теоремы можно вывести еще несколько математических соотношений:
1. Для нахождения гипотенузы:
с = a²+b²
2. Для нахождения одного из катетов:
a = c²-b²
b = c²-a²
Доказательство теоремы Пифагора
Сегодня существует более 300 различных доказательств известного утверждения. Мы приведем несколько самых известных. За основу возьмем треугольник ABC с катетами a, b и гипотенузой c.
Геометрическое доказательство с квадратами
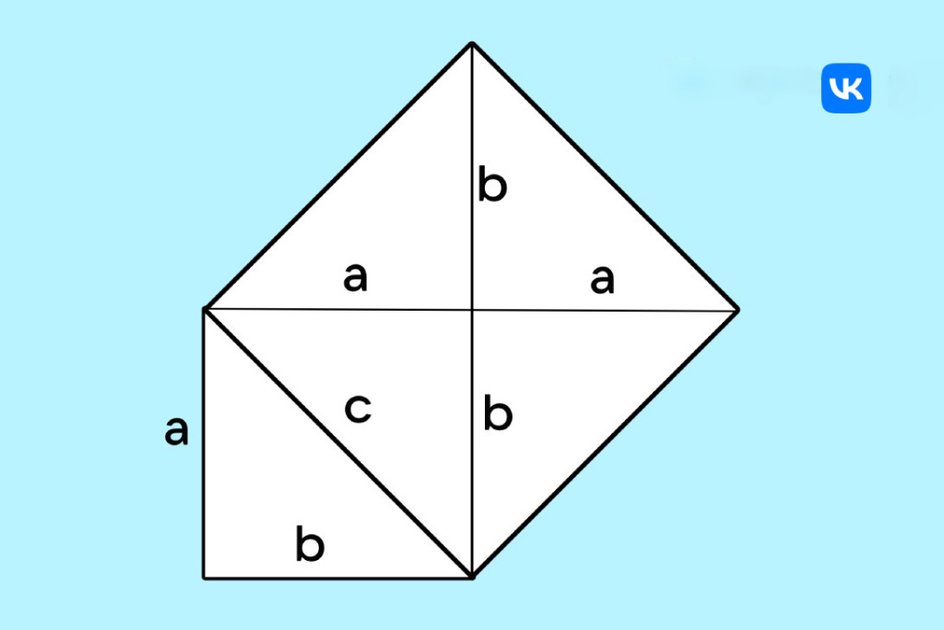
Построим на гипотенузе треугольника квадрат со стороной c. Внутри него разместим четыре одинаковых прямоугольных треугольника, у каждого из которых будут катеты a и b. Эти треугольники будут расположены так, что образуют внутренний квадрат со стороной (b – a).
Площадь большого квадрата равна c², а площадь четырех треугольников: 4 × ½ab = 2ab.
Тогда площадь внутреннего квадрата равна (b – a)².
Таким образом, можно записать равенство площадей:
c² = 4 × ½ab + (b – a)².
Если раскрыть скобки и упростить пример, получится: a² + b² = c².
Алгебраическое доказательство
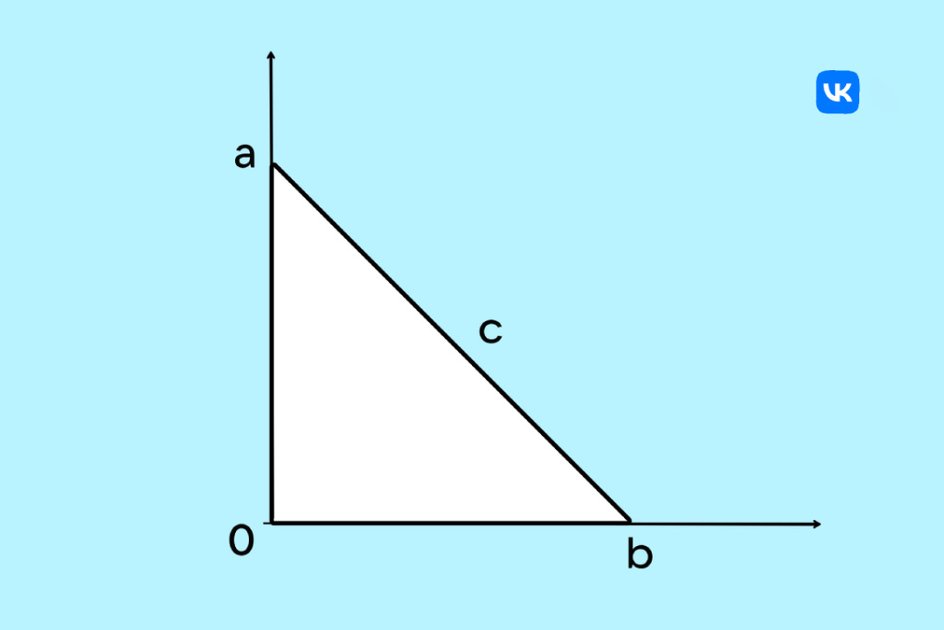
Разместим наш треугольник на системе координат: один катет будет совпадать с осью x, а другой — с осью y. Координаты вершин будут: (0, 0), (a, 0), (0, b).
Длину гипотенузы можно найти по формуле расстояния между двумя точками (3):
c = √((a – 0)² + (0 – b)²) = √(a² + b²).
Если возведем обе стороны в квадрат, получим:
c² = a² + b²
Доказательство с помощью подобия треугольников
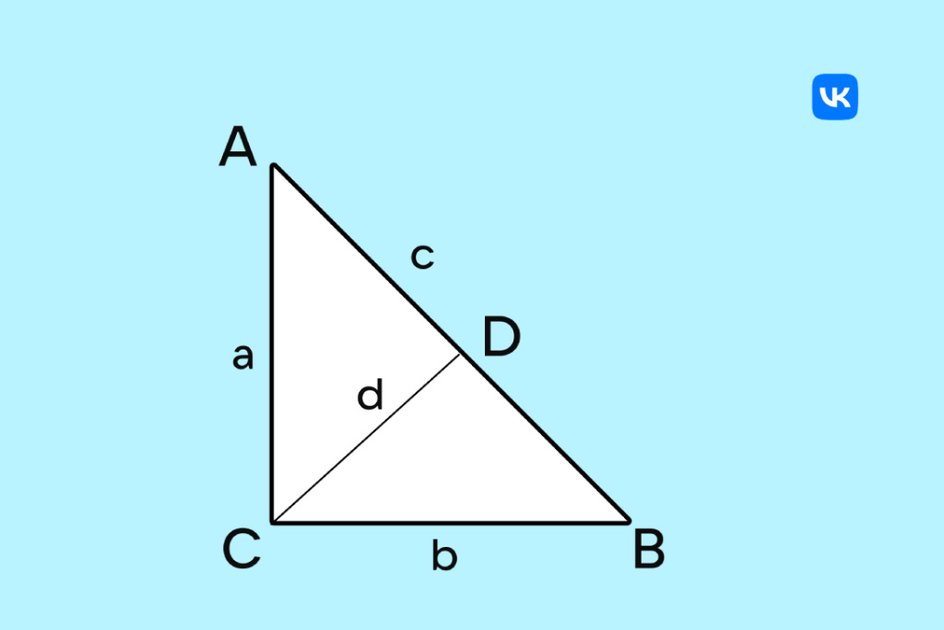
Проведем высоту CD из вершины C на гипотенузу AB. Получатся два меньших прямоугольных треугольника ADC и BDC, которые подобны исходной фигуре.
По теореме о свойствах подобия треугольников можно вывести следующее соотношение:
a/c = d/a и b/c = d/b,
где d — высота CD.
Из этих соотношений получаем:
- d = a²/c
- d = b²/c.
Приравнивая два выражения для d и умножая на c, получаем:
a² + b² = c².
О чем гласит обратная теорема Пифагора
В геометрии также существует перевернутая версия известного утверждения, или теорема Пифагора для обратных величин.

Применяя формулу древнегреческого математика, можно установить, считается ли тот или иной треугольник прямоугольным. Если сумма квадратов двух сторон будет равна квадрату третьей, значит, один из углов фигуры составляет 90°. Если соотношения не равны, значит, перед нами обычный, а не прямоугольный треугольник.
Формула и доказательство обратной теоремы Пифагора
В основе утверждения лежит та же известная формула: a² + b² = c².
Если в треугольнике со сторонами a, b и c выполняется условие a² + b² = c², то один из углов равен 90°.
Доказательство теоремы приводит Дарья Дейген, эксперт ЕГЭ, преподаватель математики, заместитель директора Университетской гимназии МГУ:
— Рассмотрим треугольник со сторонами 3, 4 и 5. Подставим длины в выражение a² + b² = c². Получим:
52 = 42 + 32
25 = 16 + 9
25 = 25
То есть получаем верное равенство. Значит, стороны треугольника удовлетворяют условию обратной теоремы Пифагора, поэтому этот треугольник является прямоугольным.
Примеры задач с теоремой Пифагора
Эту тему изучают на уроках геометрии в восьмом классе. Приведем несколько задач с теоремой Пифагора, чтобы научиться правильно применять формулу.
Найти гипотенузу
Условие: прямоугольный треугольник с катетами, равными 12 и 35 см. Найдите длину гипотенузы.
Решение:
Используем теорему Пифагора: a² + b² = c²
Подставим значения катетов и решим пример:
(12 × 12) + (35 × 35) = 144 + 1225 = 1369
√1369 = 37
Ответ: гипотенуза равна 37 см.
Найти катет
Условие: в треугольнике одна сторона равна 6 см, а гипотенуза — 10 см. Найдите длину второго катета.
Решение:
Пусть длина второй стороны — b.
По теореме Пифагора:
10² = 6² + b²
100 = 36 + b²
b² = 100 – 36 = 64
Следовательно:
b = √64 = 8 см
Ответ: длина катета равна 8 см.
Задача на обратную теорему Пифагора
Условие: в треугольнике одна сторона равна 5 см, а другая — 12 см. Является ли этот треугольник прямоугольным?
Решение:
Проверим по обратной теореме Пифагора. Пусть гипотенуза — c:
c² = 5² + 12² = 25 + 144 = 169
Следовательно:
c = √169 = 13 см
Так как сумма квадратов катетов равна квадрату гипотенузы, этот треугольник является прямоугольным.
Пифагоровы тройки
— Это наборы из трех целых положительных чисел, которые удовлетворяют уравнению теоремы Пифагора, — объясняет эксперт Дарья Дейген.
Приведем некоторые пифагоровы тройки в таблице.
| a (катет) | b (катет) | c (гипотенуза) |
| 3 | 4 | 5 |
| 5 | 12 | 13 |
| 8 | 15 | 17 |
| 7 | 24 | 25 |
| 9 | 40 | 41 |
| 12 | 35 | 37 |
| 13 | 84 | 85 |
| 16 | 63 | 65 |
| 20 | 21 | 29 |
| 20 | 99 | 101 |
| 28 | 45 | 53 |
| 33 | 56 | 65 |
| 36 | 77 | 85 |
| 39 | 80 | 89 |
Мнение эксперта
— Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов, — уточнила Дарья Дейген. — Разберем это утверждение подробнее. В прямоугольном треугольнике один угол прямой, то есть равен 90°. Сторона, лежащая напротив прямого угла, называется гипотенузой. Это самая длинная сторона в прямоугольном треугольнике. Две другие называются катетами.
Пусть длины катетов равны a и b, а длина гипотенузы — c. Тогда теорема Пифагора выглядит следующим образом:
c² = a² + b²
— Чтобы ускорить вычисления, полезно помнить про пифагоровы наборы чисел и использовать таблицы с ними в школе, — советует эксперт.
Что нужно запомнить о теореме Пифагора
Эта простая формула помогает решить много практических задач и научиться лучше разбираться в геометрии. Собрали основную информацию про теорему Пифагора:
- О соотношении сторон в прямоугольном треугольнике было известно с древних времен. Математик и философ Пифагор доказал, что в такой фигуре сумма квадратов катетов равна квадрату гипотенузы.
- Формула теоремы Пифагора: c² = a² + b²
- Обратное утверждение тоже верно: если в каком-либо треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник — прямоугольный.
- Три натуральных числа, которые подходят под условия теоремы Пифагора, называются пифагоровой тройкой. Их используют, чтобы ускорить решение задачи.
Список источников:
- Глейзер Г. О теореме Пифагора и способах ее доказательства. Математика, № 24. 2001.
- Диоген Лаэртский. О жизни, учениях и изречениях знаменитых философов. Под ред. А. Лосева. 1979.
- Яковлев И. Материалы по математике.
Эксперт: Дарья Дейген, эксперт ЕГЭ, преподаватель математики, заместитель директора Университетской гимназии МГУ







